Playing with Go: a concurrent quicksort
A little while ago google released a concurrent programming language called go that appeals to my curiosity as both an academic and a guy who likes to write code. I road tested it by coding up a concurrent quicksort implementation. This summarizes my generally positive impressions of the language.
Go appeals to me as an academic because it supports the CSP concurrency model. CSP, introduced in a paper by C. A. R. Hoare, is a programming system that supports concurrent threads that interact primarily by sending synchronous messages. The synchronous messages are unusual in that a message is never in flight. Sender and receiver have to both stop to exchange the data, so a message exchange is a combination of synchronization – like acquiring a lock – and data exchange. In order to put more concurrency into a system where both parties to a data exchange have to synchronize, CSP introduces non-determinism to some language constructs involvoing communication requests. A programmer can say “I’ve got three messages to send out. If any of the receivers is ready, send to them, and if more than one is ready I have no preference for which message you send.”
This combination encourages designers to think in unusual ways and it’s a fun paper to expose students to. I’ve often wanted to sit down and code up some algorithm in CSP and see how well the model really works. Go is probably the highest profile CSP-ish implementation, so it’s attractive. I say CSP-ish because it keeps the spirit of the paper but extends the ideas in practical ways – communication channels are made independent of thread names and allow multiple threads to communicate on a channel; non-determinism is extended to both reading and writing; things like that.
Before I talk about Go, I’m going to review quicksort and how to make it concurrent.
Quicksort
Quicksort is a fast sorting algorithm that is amenable to concurrent implementation. Until I sat down to write this, it hadn’t occurred to me that the quicksort was also created by C. A. R. Hoare. What that means – other than Hoare is a smart guy – I don’t know, but I have a sudden desire to try to work monitors in here as well.
Quicksort is based on the clever observation that one can sort an array by partitioning the elements around a pivot element and then doing the same to each of the partitions. The partitioning step consists of picking an pivot element in the array, p, and moving the elements in the array around so that all the elements less than p have indices less than p and vice versa. Partitioning will usually move several array elements, including p, around. Notice that the partitioning has put p into the place it belongs in the array – no element will ever move from the set that’s smaller than p to the set that’s larger; once a partitioning step is complete, its pivot element is in its sorted position.
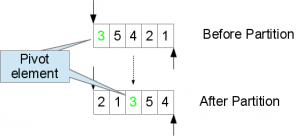
The diagram below illustrates partitioning on a small array of 5 integers (1 through 5). The two arrows indicate the range of the array to partition (the whole array) and the pivot element is in green. We arbitrarily pick the first element as the pivot here. The array on top is the array before partition, and the one on the bottom (below the dotted line) is the partitioned array.
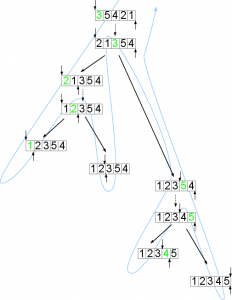
Quicksort is a recursive algorithm – an algorithm that repeats the same procedure on sub-problems to get the answer. Once the partitioning step is completed, the process starts over again on the two sub-arrays on either side of the pivot element. The pivot element is in the right place, so it is in neither sub-array. A partition step on a one-element array or a zero element array returns immediately, without partitioning the sub-arrays. The figure below shows the complete sorting of our 5 element array using quicksort.
Time goes from top to bottom of that diagram, so the final, sorted array is the bottom array (on the right). Each dotted line is a partition step, and each pair of solid lines is the recursive step of partitioning the sub-arrays. Each partition step is carried out on the sub-array defined by the arrows that touch the array at that step. The single thread of control follows the blue arrow.
The quicksort algorithm has been studied a lot and is the basis of most in-memory sort routines. It is also amenable to a concurrent implementation. Each step in the recursion – each time the partitioning routing is called – operates on an independent subarray. That’s the observation that leads directly to a concurrent implementation, as we’ll see below.
Concurrent Quicksort
My simple concurrent implementation – and I’m sure I’m not the first to do it – uses a collection of worker threads and a coordinator thread. The coordinator sends a message to an idle worker telling it to sort the array and waits to receive messages from the workers about the progress of the algorithm.
A worker partitions a sub-array, and every time that worker gets ready to call the partition routine on a smaller array, it checks to see if there is an idle worker to assign the work to. If so, it sends a message to the worker to start working on the sub-problem; if not the current worker makes calls the partition routine itself.
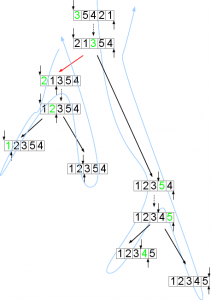
After each partitioning, two recursive calls are (usually) made, so there are plenty of chances to start other workers. The diagram below shows two workers sorting the same 5-element array. Each blue line represents the flow of control of a worker thread, and the red arrow represents the message sent from one worker to start the other. (Since the workers proceed working concurrently, it is no longer guaranteed that the smaller elements in the array will be ordered before the larger; what is certain is that the two workers will never try to manipulate the same elements.)
A worker can complete working either because it has directly completed all the work sorting the subarray it was initially called on, or because it has ordered a subset of that array but has passed some or all of the remaining work to other workers. In either case, it reports the number of elements it has ordered back to the coordinator. (The number of elements a worker has ordered is the number of partitions of sub-arrays that have 1 or more members).
When the coordinator hears that all the elements in the array have been ordered, it tells the workers that there is nothing left to do, and the workers exit.
That’s the basic idea. In the code attached, I incorporated some common optimizations to the quicksort algorithm, but the basic idea is that at every step where a worker might call the quicksort routine on a smaller sub-array, it passes that job to another worker if a worker is idle.
So, how do we do that in Go?
Implementing in Go
The whole commented package, including test code, is available. I’m only going to talk about the parts of it that coordinate the multiple workers traversing and sorting the array. Most of the code snippets below are directly from the package, and the one that is not is a minor simplification.
I’m not going to go into great detail about Go syntax here. The language specification, other references, and tutorials at http://golang.org are quite good.
My implementation is wrapped in a class that keeps the sorting parameters together. It holds the channels for communicating between the coordinator and the workers, and between workers, as well as the number of workers to start. In addition, when a sub-array is small enough, my implementation stops using the recursive quicksort algorithm and does a simple insertion sort to finish the job; the size of “small enough” is also stored in the class instance. The data structure that holds these looks like:
// Parameters that hold across the sort
type SortContext struct {
workers int
lim int
work chan *Chunk
done chan int
}
The number of workers to start is in workers, an integer. If a sub-array has fewer than lim elements (an integer), insertion sort is used. Idle workers listen on work, a channel that carries pointers to chunks of work; a nil Chunk means that the worker can terminate. When a worker completes a chunk of work it sends the number of array elements it put in order to the coordinator on the done channel, which carries integers. The number ordered is the number of recursive quicksort calls plus the number of elements passed to insertion sort.
Starting a worker thread in Go is as simple as prepending the go keyword to a function call. Starting a set of workers is as simple as:
// Start up a set of workers
for i := 0; i < self.workers; i++ {
go self.worker()
}
Each of those workers has access to the channels through the enclosing class structure. That loop is how the coordinator starts a concurrent sort.
The worker routine looks like this:
func (self *SortContext) worker() {
for c := range self.work {
if c == nil { break }
self.done <- self.p_qsort(c.a , c.l, c.u)
}
}
The worker loops, assigning each chunk it reads from the work channel to the c variable as it gets the chunks. If the chunk is a null pointer (nil) the worker breaks out of the loop and exits. Otherwise it calls the parallel quicksort function (p_qsort) with the array to sort and the bounds (c.l is the lower bound and c.u is the upper). That function returns the number of elements it directly ordered, which the worker sends to the done channel, and waits for the next chunk.
That’s fairly terse code, but pretty clear and idiomatic after a surprisingly short time. Of particular note is the for var := range channel idiom, which reads messages on a channel until the sender closes it. This code explicitly exits the loop because there are many potential senders on that channel; each worker may send on it, so no worker closes it.
Multiple workers can execute that loop without interfering with each other’s ability to read messages from the channel. If more than one worker is blocked on self.work and a worker sends a message on it, exactly one of the blocked workers will receive the message. There is no guarantee which, of course.
That construct makes it simple to start as many or as few workers as the environment dictates.
After starting the workers, the coordinator does this:
// Deliver the work to the first worker who listens
self.work <- &Chunk{a, 0, a.Len()}
That chunk of work is to sort the array called a from its first element to its last element. The array a (really a slice for you Go sticklers) is a parameter to the member function that started the sort.
Making that call blocks the coordinator until a worker starts listening for a chunk of work. As soon as one blocks to receive a chunk, that first chunk is delivered, the worker starts working and the coordinator moves on to:
// Count up the ordered elements
for i:=0 ; i < sz; {
i += <-self.done
}
The coordinator waits for each worker to report completion of each chunk of work it does. When the whole array is sorted (sz is set to the total elements in the array), that loop terminates and the coordinator shuts down the workers by sending them all a nil chunk of work.
// Tell the workers to terminate
for i := 0; i < self.workers; i++ {
self.work <- nil
}
The only thing left to sketch is how workers start other workers. After each partition step, a worker has (at most) 2 sub-arrays that need to be partitioned. For each subp-array this worker does the following (where l and u are the lower and upper bound of the subarray to be partitioned):
select {
case self.work <- &Chunk{a, l, u}:
default:
rv += self.p_qsort(a, l, u)
}
The select statement will send the message (self.work <- &Chunk... ) if there is a worker listening on self.work. If not, the code will choose the default branch, which is a recursive call on self.p_qsort.
A couple details: The case: self.work ... line is guarding an empty block after the colon. If statements followed it, they would be executed after the message was successfully sent. No such additional statements are required here. In the default: branch, the rv += ... adds the number of elements ordered by the recursive call to the number ordered so far in this call. This routine will return rv to the caller and eventually to the coordinator. You can see how that works in the complete code.
The select is actually slightly simplified from the running code, which includes another bypass used when the insertion sort is invoked. Again, see the complete code.
This use of select is a particularly convenient construction. It is short enough that converting the recursion in the serial version to the choice of recursing or starting a worker in the concurrent version does not interrupt the flow of the code.
More importantly, it is encoding a fairly sophisticated concurrent operation – “hand this work off if there is an idle worker, but do it in this worker if not” – succinctly and idiomatically. One can perform the operation in conventionally threaded languages, like java, but each programmer generally rolls their own mechanism to implement it. That extra activation energy often gets the better of programmers. Go encodes the construction so simply that one hopes programmers will use it more often.
Seeing For Yourself
The code includes a couple benchmarks that can show that this implementation does take advantage of multiple processors. To run it, install the source in your GOPATH and compare
$ go test -test none -bench '.*' psort
$ go test -cpu 4 -test none -bench '.*' psort
On my 4-core i5 the results look like:
$ go test -cpu 1 -bench .\* -run none psort PASS BenchmarkOneWorker 1 4176997000 ns/op BenchmarkFourWorkers 1 4104459000 ns/op BenchmarkTenWorkers 1 4220084000 ns/op ok psort 12.655s $ go test -cpu 4 -bench .\* -run none psort PASS BenchmarkOneWorker-4 1 4165567000 ns/op BenchmarkFourWorkers-4 1 1633784000 ns/op BenchmarkTenWorkers-4 1 1632001000 ns/op ok psort 7.526s
Each of these benchmarks sorts 5 million integers. That’s one “op.” The BenchmarkOneWorker benchmark uses one worker thread and takes about 4.2 seconds to sort the array; BenchmarkFourWorkers uses 4 workers and BenchmarkTenWorkers uses 10.
In the first invocation, with -cpu 1, only uses one CPU, so no matter how many workers are used, there is no speedup. In the second invocation, with -cpu 4, adding workers adds CPUs, so there is an appreciable speedup, though not completely linear.
Feel free to play around with it or use it in projects, but there are corner cases where it will perform badly.
Closing Remarks
Overall I was pleased with the concurrency support. It did take some time, but the language and features do lead a programmer toward efficient abstractions.
The documentation often repeats the phrase “communicating for concurrency” which is an excellent guiding principle for getting the most out of Go. I went down a couple blind alleys when I tried to do other things, like start as many goroutines as possible without communicating between them, or letting many messages pile up in buffered channels hoping that a goroutine would finally get around to reading them. Neither of those works as well as sending a message when an idle worker is listening, which is the direction Go pushes you.